Относительные скорости: суша и вода

Относительные скорости: суша и вода

Теперь представим сочетание суши и воды, начиная с неподвижной стоячей воды, скажем, в озере. Некто гребет на лодке по озеру со скоростью 5 км/ч — это та же средняя скорость пешехода на суше. Его скорость — 5 км/ч относительно воды; но поскольку вода стоячая, т. е. она не движется относительно берега, окружающего озеро, скорости будут всегда такими же, как и по отношению к воде.

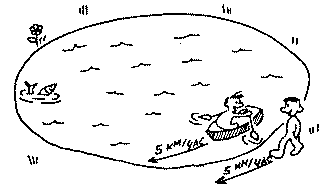
Говоря более сухим научным языком: т. к. относительная скорость воды по отношению к земле равна нулю, скорость лодки по отношению к обоим стихиям (земле и воде) будет всегда одинакова, как бы она ни была направлена, потому что прибавление или вычитание нуля не меняет нашей цифры. Если озеро круглое, диаметром 5 км, то переплыть его по самому широкому месту в любом направлении займет у гребца один час. Если он гребет вдоль берега со скоростью 5 км/ч, а его друг идет пешком по берегу рядом с ним тоже со скоростью 5 км/ч, их скорость по отношению друг к другу будет нулевой, и они смогут поболтать как следует, как если бы они шли рядом или сидели в лодке вместе:

Предположим теперь, что водная среда не является неподвижной, как в озере, а представляет поток в реке, текущий со скоростью 3 км/ч относительно берега. Вся картина и вычисления становятся теперь более сложными.

Человек в лодке по-прежнему гребет со скоростью 5 км/ч относительно воды, но вода также движется с ним со скоростью 3 км/ч относительно берега. Если он гребет против течения, то его "водная скорость" будет по-прежнему 5 км/ч, но встречный поток в 3 км/ч уменьшит ее до 5-3 = только 2 км/ч относительно берега (его "земная скорость"). Если его друг и сейчас идет пешком по берегу рядом с ним, то ему нужно выдерживать скорость всего в 2 км/ч (по отношению к земле), чтобы сохранить положение рядом с лодкой.

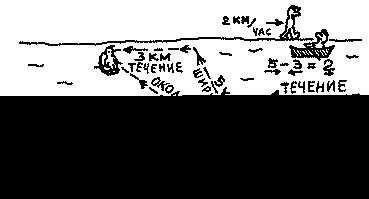
Но если человек в лодке гребет вместе с потоком, его скорость относительно земли будет 5 км/ч, которых он достиг на веслах плюс 3 км/ч, которые добавляет течение, что даст 5+3=8 км/ч по отношению к берегу. Его друг теперь должен идти весьма резво, со скоростью 8 км/ч, чтобы оставаться с ним.

Итак, наша лодка попутешествовала вдоль и против течения. Теперь посмотрим, что произойдет, если гребец предпримет путь поперек течения, пересекая реку так, что нос ее ориентирован под прямым углом к берегам. Пусть река имеет ширину 5 км — в этом случае для ее перемещения лодке потребуется 1 час. Но попадет ли она в точку, напротив точки старта? Нет, не попадет, а окажется далеко от нее, и если точнее, то на расстоянии 3 км, потому что на это расстояние ее снесет течение скоростью 3 км/час за время пересечения реки, равное одному часу.

Пожалуйста, заметьте, что хотя гребец приложил усилия только для перегона лодки на расстояние 5 км по неподвижной воде, течение увеличило пройденное расстояние за 1 час почти до б км, в то время, как скорость лодки относительно воды осталась равной 5 км/ч.