Понятие о степенях свободы

Понятие о степенях свободы

Человек изучает окружающий мир для того, чтобы приспособить его к себе, сделать безопасным для себя свое существование в нем. Поэтому процесс человеческого познания специфичен по целям, объекту и методам исследования.

Изучая какое-то явление природы, человек выделяет из всего многообразия связей и сторон этого явления то, что его больше всего интересует, и создает в своем сознании мысленный образ, идеальный объект. Этот объект можно считать некоей моделью, наблюдая за которой, изучают качественные и количественные закономерности ее поведения.

Таблица 1

Эксперименты с идеальным объектом позволяют обнаружить количественные взаимосвязи, так называемые физические законы.

Эти рассуждения можно представить в виде схемы (таблица 1).

В механике при изучении движения различных физических объектов используются следующие модельные представления: материальная точка, абсолютно твердое тело, система материальных точек или тел.

Простейшей моделью является материальная точка – тело, размерами которого в данных условиях движения можно пренебречь. В этом определении слова «в данных условиях движения» означают, что одно и то же тело при определенных его движениях можно считать точкой, а при других нельзя.

Понятие материальной точки абстрактное, но его введение облегчает решение многих практических задач. Например, океанский лайнер крайне мал по сравнению с протяженностью его рейса, и поэтому корабль можно считать точкой при описании движения в океане. Точно так же материальной точкой можно представить самолет или ракету, изучая их поступательное движение по заданным траекториям. Движение тел происходит в пространстве и во времени (t). Поэтому положение материальной точки определяется по отношению к какой-либо другой произвольно выбранной точке, называемой точкой отсчета или началом координат.

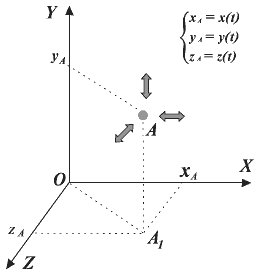
Пусть это будет точка О (рис. 1). Проведя через нее три взаимно перпендикулярные оси О_х, О_у и O_z, получим прямоугольную систему координат, в которой положение материальной точки А (например, положение самолета в воздухе) в данный момент времени характеризуется тремя координатами x_A, y_A, z_A.

Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы.

Итак, если материальная точка (рис. 1) свободно движется в пространстве и изменяются ее координаты х, у, z, то она обладает тремя степенями свободы. Если точка В движется по некоторой поверхности (рис. 2) и изменяются ее координаты х, у, то она обладает двумя степенями свободы. Наконец, если точка С движется вдоль любой из осей координат, то она имеет одну степень свободы.

Кажется, к этому нечего добавить. Однако в действительности оказывается, что представление о степенях свободы складывается совсем не просто. Известный ученый-биолог Бернштейн Н. А, великолепно владевший умением рассказывать просто о сложных явлениях, в своей популярной книге о природе движения[3] пишет:

«Современная техника создала машины огромной сложности, способные совершенно самостоятельно, без участия человека, выполнять самые разнообразные и непростые операции. И самое поразительное, что все эти машины-автоматы при их сложности и изобилии подвижных частей имеют по одной-единственной степени свободы, т. е. обладают тем, что в технике называют вынужденным движением. Это значит, что каждая движущаяся точка в этих машинах, каждая деталь рычага, тяги или колеса движется все время по одному и тому же строго определенному пути. Форма этого пути может быть очень разнообразной: у одних точек – круговой, у других – прямолинейной, у третьих – овальной и т. д., но с этого пути движущаяся точка не сходит никогда. Таким образом, машины-автоматы в смысле своей подвижности принадлежат к числу самых простых систем, какие только могут существовать».

Н. А. Бернштейн

Утверждение об «одной единственной степени свободы» машины-автомата нуждается в оговорке.

Не стоит, по-видимому, говорить о подвижности машины-автомата вообще, в целом, а следует говорить только о подвижности какой-то движущейся детали этой машины.

И тогда здесь, на первый взгляд, обнаруживается некоторое противоречие. Если точка В (рис. 2) движется по дуге окружности в плоскости ХОY, то ее положение в каждый момент времени описывается двумя независимыми координатами x_B, y_B. Казалось бы, точка В имеет две степени свободы. Но это справедливо только для свободного движения. Если же движение является вынужденным, например, возвратно-поступательным, и «с этого пути движущаяся точка не сходит никогда», то эта точка имеет одну степень свободы.

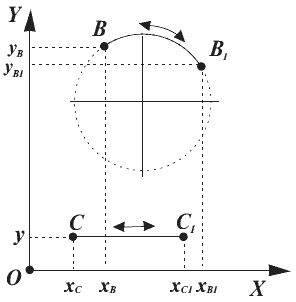
Рис. 2

Вернемся к образным рассуждениям Бернштейна:

«Если бы какая-нибудь часть такой машины получила вместо одной две степени свободы, это совсем не значило бы, что на ее долю вместо одного достались два или даже несколько возможных путей-траекторий. Нет, это означало бы, что даная часть машины получила возможность „разгуливать“ по какой-то поверхности. Если я возьму перо и стану водить им по поверхности листа бумаги, то, какие бы фигуры ни вздумалось мне им изображать, я нигде не превышу своих возможностей по части дозволенных кончику пера двух степеней свободы, пока буду водить его без отрыва от бумаги. Этот переход от одной степени свободы к двум означает, таким образом, огромный качественный скачок от одной-единственной, точно определенной дорожки-траектории к бесконечному и вполне произвольному разнообразию таких дорожек… Три степени свободы вместо двух дают еще больше, хотя на этот раз не происходит такого огромного качественного скачка, как при переходе от одной к двум степеням свободы… Для пояснения надо сказать, что совершенно ничем не связанная точка, например, вольно порхающая в воздухе снежинка, не может иметь больше трех степеней свободы».

При решении практических задач очень часто оказывается, что в данных условиях движения никак нельзя пренебречь размерами тела. Тот же океанский лайнер при исследовании воздействия на него водной стихии (например, при бортовой и килевой качке) материальной точкой уже никак не назовешь, его следует рассматривать как тело конечных размеров.

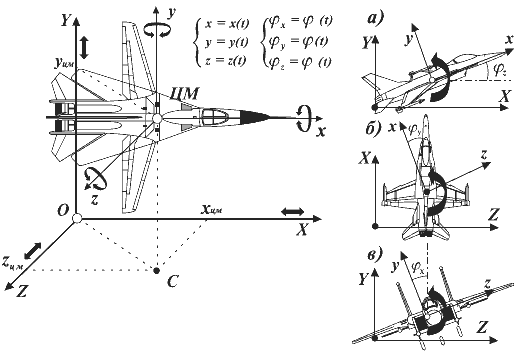
Рис. 3

По этой причине в механике вводится еще одна модель – абсолютно твердое тело, то есть тело конечных размеров, которое ни при каких условиях не деформируется (не изменяет свою форму и размеры).

Эта модель существенно отличается от предыдущей. Она позволяет любое движение тела рассматривать как комбинацию поступательного и вращательного движений.

Следовательно, если твердое тело свободно движется в трехмерном пространстве, то оно получает дополнительные три степени свободы, а именно: свободы вращения (поворота) тела относительно каждой из осей координат. А это означает, что всякое твердое тело по сравнению с материальной точкой обладает шестью степенями свободы.

Перемещения тела при поступательном и вращательном движениях измеряются различно. При поступательном движении их можно определить по линейному перемещению любой точки тела, например, его центра масс (ЦМ), в неподвижной системе координат.[4] А при вращательном движении – по углу поворота тела относительно соответствующей координатной оси. Для измерения углов в центре масс тела помещают начало другой, подвижной системы координат, оси которой первоначально ориентированы так же, как и оси неподвижной системы. При повороте тела положение осей этой связанной системы координат относительно неподвижной системы определяется тремя углами.

Так, например, при изучении движения самолета в трехмерном пространстве (рис. 3) рассматривают:

• во-первых, движение его центра масс как материальной точки с массой, равной массе самолета, в неподвижной (земной) системе координат XYZ;

• во-вторых, поворот самолета как твердого тела конечных размеров относительно центра масс.

Положение осей связанной системы хyz, а следовательно, и повороты самолета в земной системе координат определяются тремя углами: ?х, ?y, ?z.

И, наконец, в механике часто используется еще одно модельное представление: связанная система тел – совокупность материальных точек или тел – рассматриваемая как единое целое. Такая система имеет общий центр масс, а число степеней свободы системы обусловливается количеством связей между отдельными ее частями.

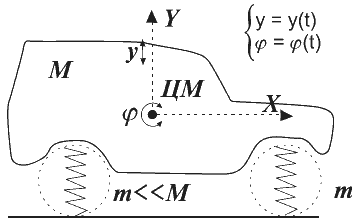
Рис. 4

Житейским и понятным примером такой модели может служить автомобиль, кузов и колеса которого образуют взаимосвязанную механическую систему.

Рассмотрим самую простую схему двухосного агрегата, в которой кузов опирается на колесный ход через упругие устройства (например, цилиндрические пружины).

При движении по неровностям дороги возникают колебания автомобиля.

Кузов автомобиля (подрессоренная масса М) колеблется с некоторой частотой w в этих колебательных движениях и, как всякое твердое тело конечных размеров, имеет шесть степеней свободы. Колеса автомобиля (неподрессоренные массы m1) тоже колеблются, но с большей частотой (wk>w).

Если автомобиль имеет независимую подвеску колес, обеспечивающую только их вертикальные перемещения, то колеса имеют по одной степени свободы. Легко догадаться, что в рассматриваемом случае движущийся по неровной дороге четырехколесный автомобиль, рассматриваемый как колебательная механическая система тел, имеет десять степеней свободы.

Принятием дополнительных упрощающих допущений можно прийти к новому модельному представлению автомобиля – к плоской расчетной схеме (рис. 4), имеющей всего две степени свободы движения кузова относительно ЦМ.

Данный текст является ознакомительным фрагментом.